Notes on RoFormer: Enhanced Transformer with Rotary Position Embedding

• RoPE overcomes limitations of its 2 precursors: Absolute and Relative Positional Embedding
• It takes the best-of-both-worlds approach
  • Encodes absolute positions using rotation matrix
  • Incorporates relative positions into the attention matrix
• Offers 3 benefits:
  • Flexibly adapts to work for any sequence length
  • Decays the inter-token dependency as relative distance increases
  • Equips linear self-attention with relative position encoding

Absolute Positional Embedding

• Input embeddings fed to transformer only convey meaning of token in isolation
• We want model to treat nearby words as nearby and distant words as distant
  • Important because self-attention is position invariant
• Represent the above in a manner that model can understand
• PE values are only computed once and reused for every sentence during both training and inference
• All we have to do is add these PE values with input embeddings, which change for every sentence

Source: Umar Jamil, Attention is all you need (Transformer)

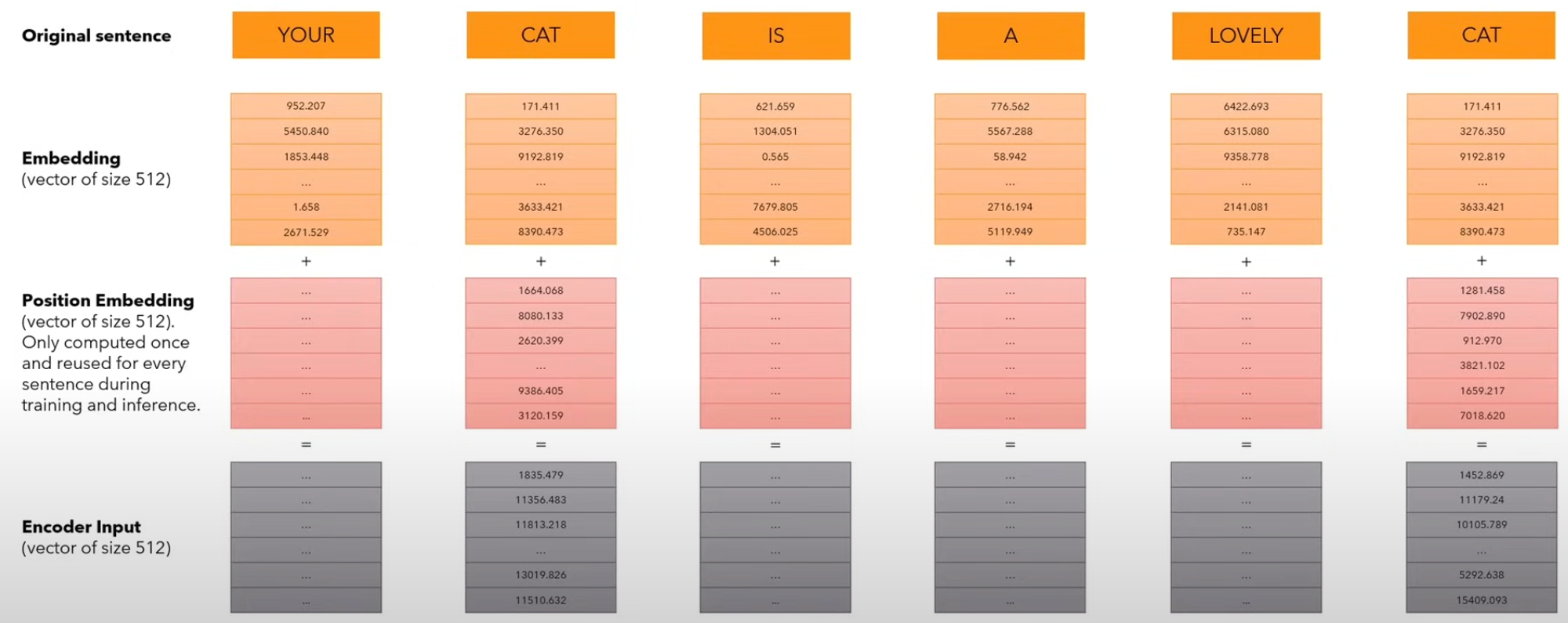
\[EncoderInput[i]= Embedding[i] + PositionalEmbedding[i]\]

📝 Formulation

\[f_{t: t \in\{q, k, v\}}(\boldsymbol{x}_i, i):= \\ \boldsymbol{W}_{t: t \in\{q, k, v\}}(\boldsymbol{x}_i, \boldsymbol{p_i})\]

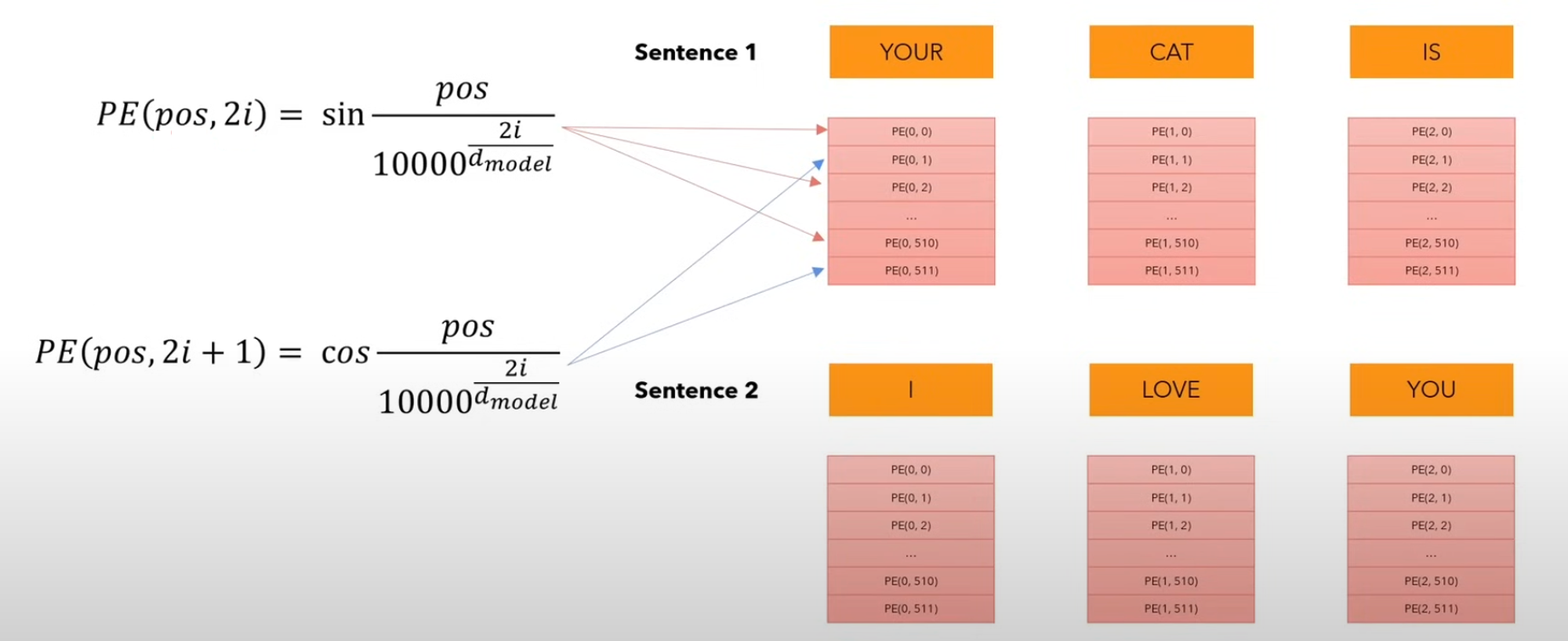
\[\begin{cases} \\ \mathbf{p}_{i, 2t} = \sin \left( k/{10000^{2t/d}} \right) \\ \mathbf{p}_{i, 2t+1} = \cos \left( k/{10000^{2t/d}} \right) \end{cases}\]

Source: Umar Jamil, Attention is all you need (Transformer)

✍🏻 Example

• \(PE(1,3)\) pertains to the second token in the sentence and the fourth value of the token embedding
• Hence we use, \(pos=1\), \(2i=2\) and \(cos\)

🖼️ Visual Intuition

Source: Amirhossein Kazemnejad, Transformer Architecture: The Positional Encoding

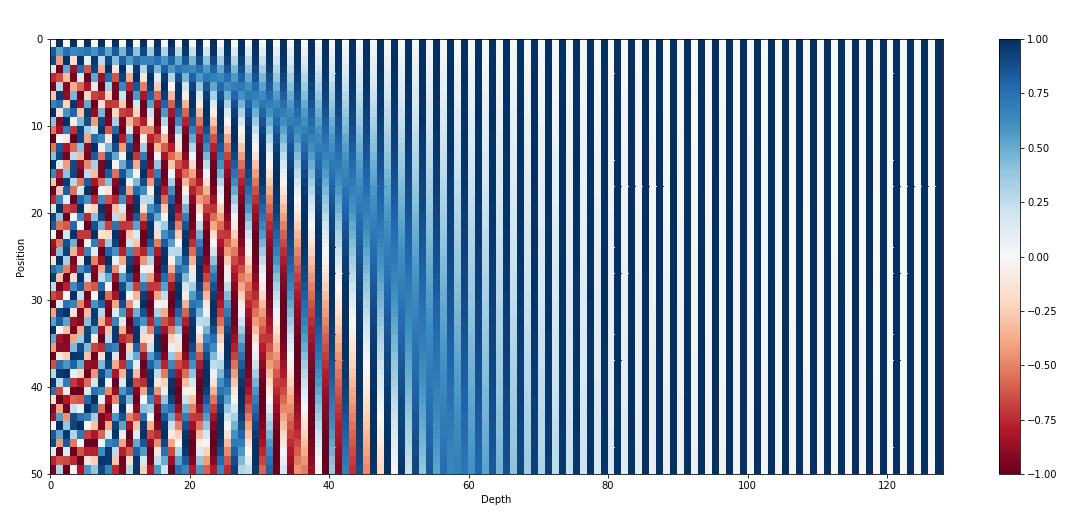
• Each row is a relative position embedding (there are 50 token positions here)
• Closer positions have visually similar encodings than farther ones

🟡 Limitations

• Sequence Length Bottleneck: We cannot represent PE values (and thereby, distance) beyond the sequence length we set (50 in the above diagram)
• Lack of Relative Positions: PE values are computed independently, hence, model treats pos 1 vs pos 2 the same way as pos 2 vs pos 100

Relative Positional Embedding (T5 model)

Source: Efficient NLP, Rotary Positional Embeddings: Combining Absolute and Relative

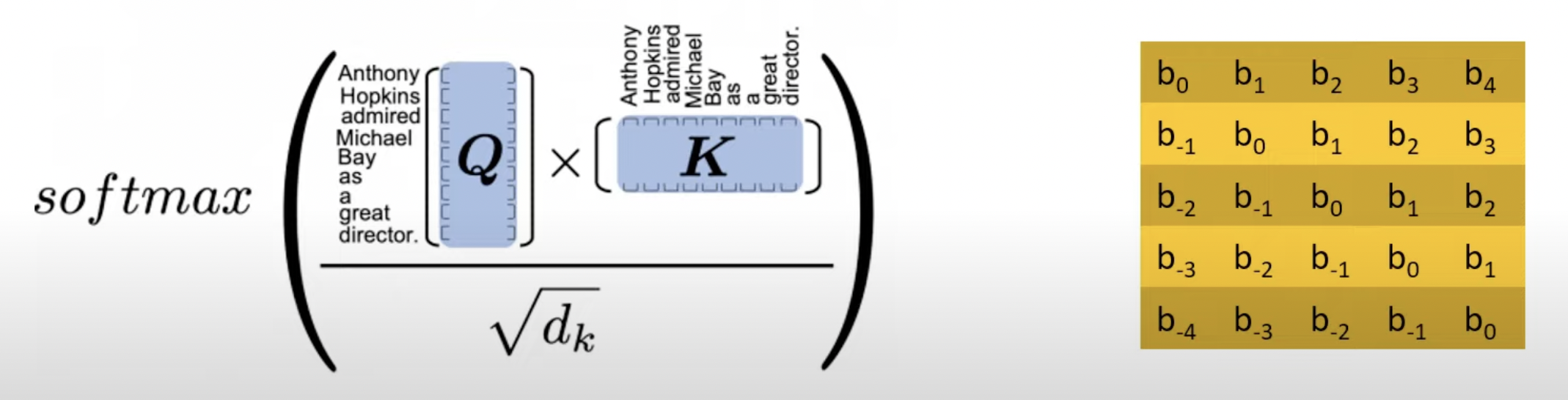
• Instead of representing a token’s position, represent a distance offset between 2 tokens using trainable parameters
  • (e.g.) \(b_2\) represents distance offset of 2

Offset/Bias Matrix

	\(Anthony\)	\(Hopkins\)	\(admired\)
\(Anthony\)	\(b_0\)	\(b_1\)	\(b_2\)
\(Hopkins\)	\(b_{-1}\)	\(b_0\)	\(b_1\)
\(admired\)	\(b_{-2}\)	\(b_{-1}\)	\(b_0\)

• Token pairs that are same distance apart have same offset value
• This offset matrix (called bias) is added to attention matrix to encode positions

\[Final Attention Matrix = Attention Matrix + Offset Matrix\]

📝 Formulation

Formulation for Absolute Position Embedding:

\[f_{t : t \in \{q, k, v\}} \left( \mathbf{x}_i, i \right) := \\ \mathbf{W}_{t : t \in \{q, k, v\}} \left( \mathbf{x}_i + \mathbf{p}_i \right)\]

Formulation expected for Relative Position Embedding:

\[\begin{aligned} f_q (\mathbf{x}_m) & := \mathbf{W}_q \mathbf{x}_m \\ f_k (\mathbf{x}_n, n) & := \mathbf{W}_k (\mathbf{x}_n + \tilde{\mathbf{p}}_r^k) \\ f_v (\mathbf{x}_n, n) & := \mathbf{W}_v (\mathbf{x}_n + \tilde{\mathbf{p}}_r^v) \end{aligned} \]

• \(\tilde{p}^k_r\) and \(\tilde{p}^v_r\) are trainable relative position embeddings
• \(r = clip(m − n, rmin, rmax)\) , is clipped due to hypothesis that precise relative position is not useful beyond a certain distance
• After a few steps, below is the form we arrive for relative position embeddings:

\[q_m^T k_n = x_m^T W_q^T W_k x_n + x_m^T W_q^T \tilde{W}_k \tilde{p}_{m-n} + \\ \mathrm{u}^T W_q^T W_k x_n + \mathrm{v}^T W_q^T \tilde{W}_k \tilde{p}_{m-n}\]

• But, later works have simplified the form 🤗
• For instance, Colin Raffel et al. “Exploring the limits of transfer learning with a unified text-to-text transformer” use:

\[q_m^T k_n = x_m^T W_q^T W_k x_n + b_{i,j}\]

• This form is similar to the one discussed for T5 model

🟡 Limitations

• Re-computation of Attention Matrix: Due to this, as sequence length increases, inference speed decreases
• Issues with KV Cache: For every new token added to sequence, embeddings for all tokens will change, effectively rendering KV Cache impractical

Notice how bias values for \(Anthony\), \(Hopkins\) and \(admired\) changed (1 more column added)

	\(Anthony\)	\(Hopkins\)	\(admired\)	\(Michael\)
\(Anthony\)	\(b_0\)	\(b_1\)	\(b_2\)	\(b_3\)
\(Hopkins\)	\(b_{-1}\)	\(b_0\)	\(b_1\)	\(b_2\)
\(admired\)	\(b_{-2}\)	\(b_{-1}\)	\(b_0\)	\(b_1\)
\(Michael\)	\(b_{-3}\)	\(b_{-2}\)	\(b_{-1}\)	\(b_0\)

🧵 Enter Rotary Positional Embedding

• Instead of adding position embeddings to token embeddings, rotate the token embeddings based on its position in the sequence
• This solves the limitations of its precursors
• ✅ Solves the issue with KV Cache because we no longer compute a separate bias matrix

Source: Efficient NLP, Rotary Positional Embeddings: Combining Absolute and Relative

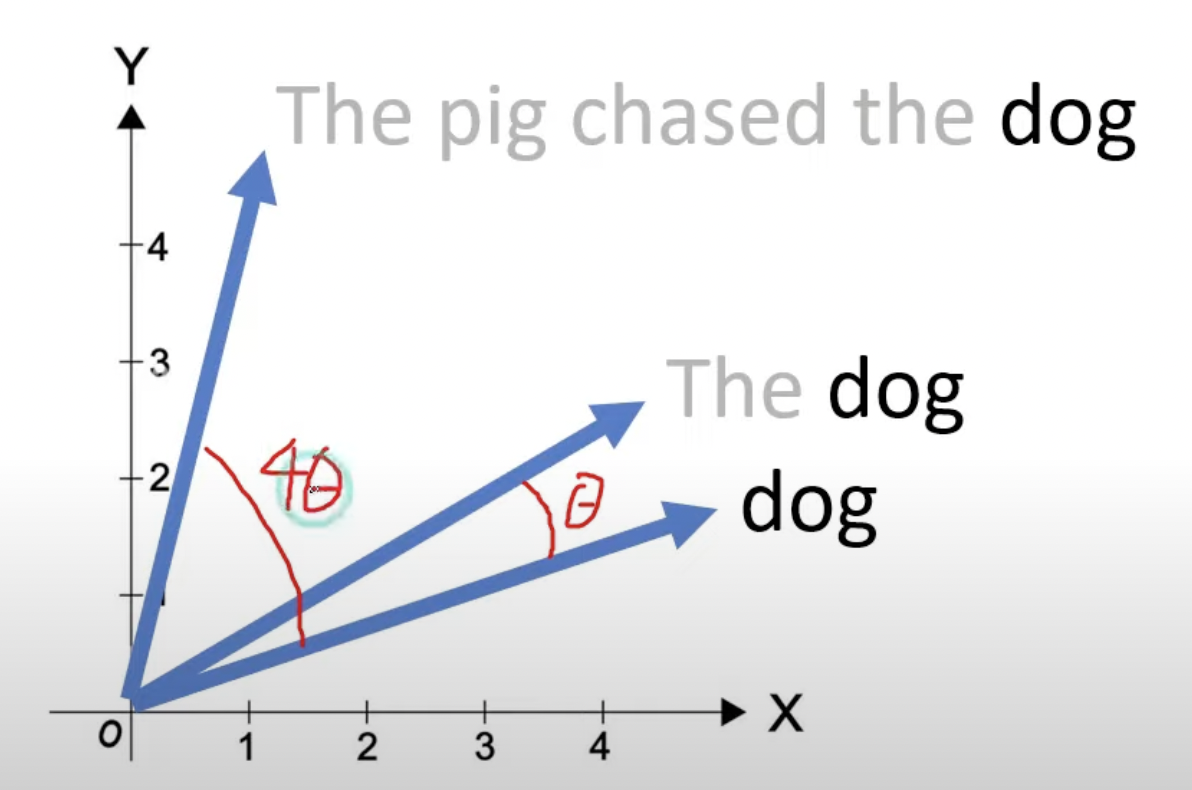
• ✅ Notion of relative distance is preserved across rotations

Source: Efficient NLP, Rotary Positional Embeddings: Combining Absolute and Relative

📝 Formulation

• Remember:

\[q_m = f_q(x_m, m)\]

\[k_n = f_k(x_n, n)\]

\[v_n = f_v(x_n, n)\]

\[a_{m,n} = \frac{\exp(\frac{q_m^\top k_n}{\sqrt{d}})}{\sum_{j=1}^N \exp(\frac{q_m^\top k_j}{\sqrt{d}})}\]

\[o_m = \sum_{n=1}^N a_{m,n}v_n\]

• In Absolute Positional Embedding method, \(q^T_m\) and \(k_n\) each encoded individual token positions
• Hence, self-attention, (aka \(q^T_mk_n\)) led to propagation of information about individual token positions
• We want to move away from that and only incorporate relative position information during the self-attention operation
  • In my understanding, it is because the absolute position is already encoded in the rotation
• In other words, we want the below to happen
  • \(q_m = f_q(x_m, m)\)
  • \(k_n = f_k(x_n, n)\)
  • \(\langle \cdot, \cdot \rangle\) denotes inner-product

\[q^T_m k_n = \langle f_q(x_m, m), f_k(x_n, n) \rangle = g(x_m, x_n, m - n)\]

• Note that \(g(\cdot)\) does not have any individual position information like \(g(\cdot, m, n)\)

Solution for 2D Case

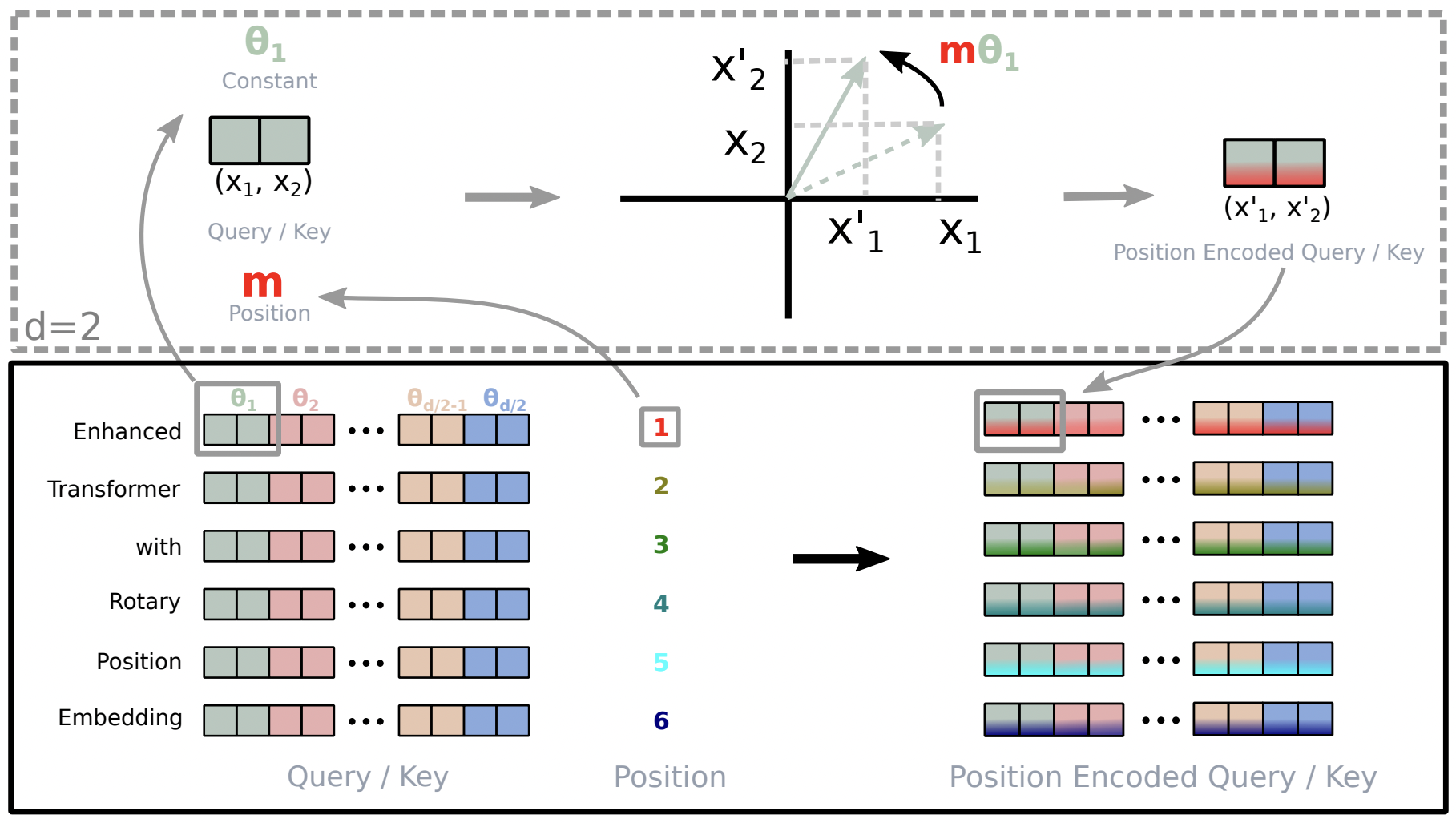
• The authors prove that, for the case of 2D vectors, the solution to the above problem is:

\[f_q(\mathbf{x}_m, m) = (\mathbf{W}_q \mathbf{x}_m) e^{im\theta}\]

\[f_k(\mathbf{x}_n, n) = (\mathbf{W}_k \mathbf{x}_n) e^{in\theta}\]

\[g(\mathbf{x}_m, \mathbf{x}_n, m - n) = \text{Re}[(\mathbf{W}_q \mathbf{x}_m)(\mathbf{W}_k \mathbf{x}_n)^* e^{i(m-n)\theta}]\]

\[f_{\{q,k\}}(x_m, m) = \begin{pmatrix} \cos m\theta & -\sin m\theta \\ \sin m\theta & \cos m\theta \end{pmatrix} \begin{pmatrix} W_{\{q,k\}}^{(11)} & W_{\{q,k\}}^{(12)} \\ W_{\{q,k\}}^{(21)} & W_{\{q,k\}}^{(22)} \end{pmatrix} \begin{pmatrix} x_m^{(1)} \\ x_m^{(2)} \end{pmatrix}\]

• Notice how first, the Key and Query are generated before rotation

Solution for General Case

• For any \(d\) dimensional input embedding, we assume \(d\) is even and divide the embedding space into \(d/2\) subspaces

\[f_{\{q,k\}}(\textbf{x}_m, m) = \textbf{R}_{\Theta,m}^d \textbf{W}_{\{q,k\}} \textbf{x}_m\]

\[ \begin{equation} R_{\Theta,m}^d = \begin{pmatrix} \cos m\theta_1 & -\sin m\theta_1 & 0 & 0 & \cdots & 0 & 0 \\ \sin m\theta_1 & \cos m\theta_1 & 0 & 0 & \cdots & 0 & 0 \\ 0 & 0 & \cos m\theta_2 & -\sin m\theta_2 & \cdots & 0 & 0 \\ 0 & 0 & \sin m\theta_2 & \cos m\theta_2 & \cdots & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & 0 & 0 & \cdots & \cos m\theta_{d/2} & -\sin m\theta_{d/2} \\ 0 & 0 & 0 & 0 & \cdots & \sin m\theta_{d/2} & \cos m\theta_{d/2} \end{pmatrix} \end{equation} \]

• This leads us to the general form of self-attention using RoPE

\[\begin{equation} \textbf{q}_m^\top \textbf{k}_n = (\textbf{R}_{\Theta,m}^d \textbf{W}_q \textbf{x}_m)^\top (\textbf{R}_{\Theta,n}^d \textbf{W}_k \textbf{x}_n) = \textbf{x}_m^\top \textbf{W}_q^\top \textbf{R}_{\Theta,n-m}^d \textbf{W}_k \textbf{x}_n \end{equation}\]

• Notice how RoPE incorporates relative position information in the self-attention step itself instead of adding it through a bias matrix like its precursor

Implementation of RoPE, all subspaces within an embedding vector are rotated by same angle

🍀 Properties of RoPE

Flexibly adapts to any sequence length

• For any new token, all we need to do is rotate its vector by \(m\theta\)
• The method is scalable and requires no pre-computation

Decay of the inter-token dependency

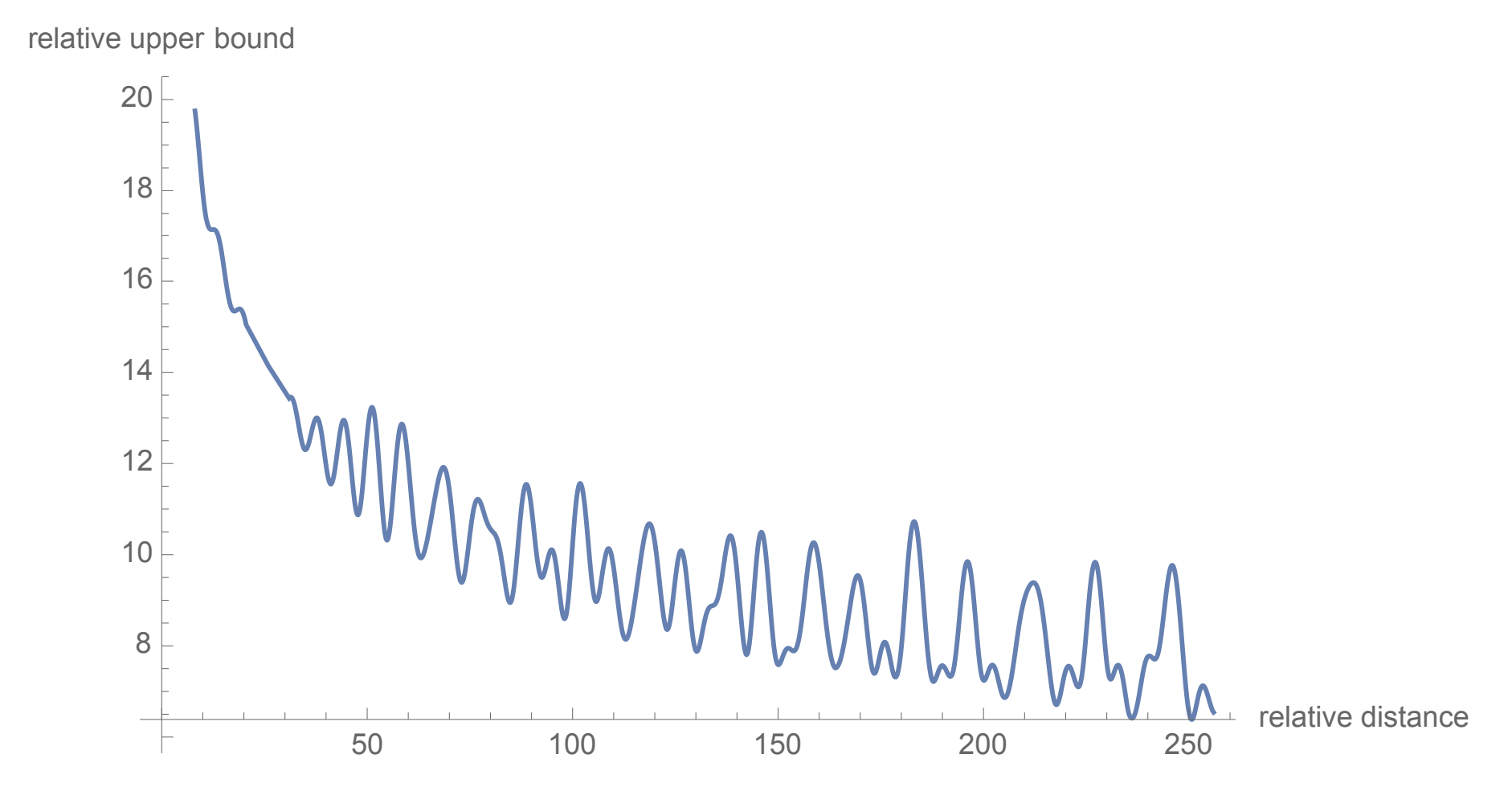
• Relative upper bound is the \(\textbf{R}_{\Theta,n-m}^d\) term in general form of RoPE: \(\textbf{x}_m^\top \textbf{W}_q^\top \textbf{R}_{\Theta,n-m}^d \textbf{W}_k \textbf{x}_n\)

Equips linear self-attention with relative position encoding

• Instead of expressing self-attention in the usual way as:

\[ \begin{equation} \text{Attention}(\textbf{Q}, \textbf{K}, \textbf{V})_m = \frac{\sum_{n=1}^N \text{sim}(\textbf{q}_m, \textbf{k}_n) \textbf{v}_n}{\sum_{n=1}^N \text{sim}(\textbf{q}_m, \textbf{k}_n)} \end{equation} \]

• Linear-attention expresses it as:

\[ \begin{equation} \text{Attention}(\textbf{Q}, \textbf{K}, \textbf{V})_m = \frac{\sum_{n=1}^N \phi(\textbf{q}_m)^\top \phi(\textbf{k}_n) \textbf{v}_n}{\sum_{n=1}^N \phi(\textbf{q}_m)^\top \phi(\textbf{k}_n)} \end{equation} \]

• The authors propose that RoPE can be combined with linear-attention simply by multiplying the rotation matrices

\[ \begin{equation} \text{Attention}(\textbf{Q}, \textbf{K}, \textbf{V})_m = \frac{\sum_{n=1}^N (\textbf{R}_{\Theta,m}^d \phi(\textbf{q}_m))^\top (\textbf{R}_{\Theta,n}^d \phi(\textbf{k}_n)) \textbf{v}_n}{\sum_{n=1}^N \phi(\textbf{q}_m)^\top \phi(\textbf{k}_n)} \end{equation} \]

Results

1. Machine Translation: WMT 2014 English -German Translation

• Evaluate English-to-German translation

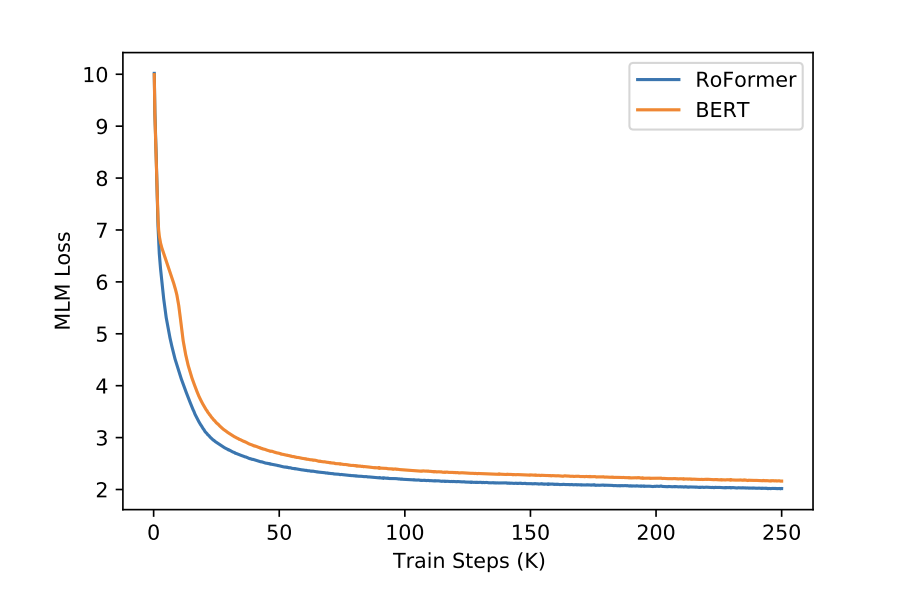
2. Pre-training Language Modeling

• Validate performance in learning contextual representations
• Pre-training dataset: BookCorpus and Wikipedia Corpus Foundation

MLM Loss - Masked Language Model Loss, (Cross-Entropy Loss)

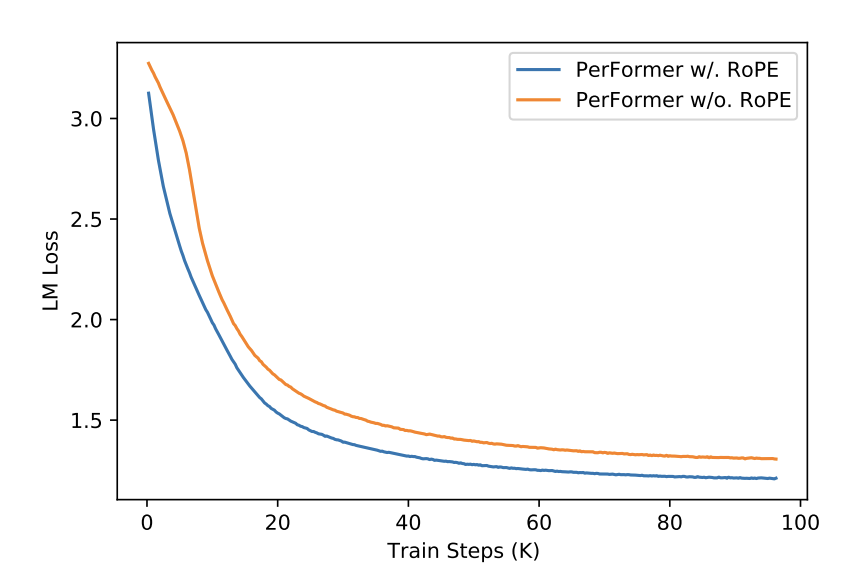
3. PerFormer + RoPE for Pre-Training

• PerFormer uses linear-attention

LM Loss - Language Model Loss, (Cross-Entropy Loss)

4. Fine-tuning on GLUE tasks

• GLUE (General Language Understanding Evaluation): Benchmark for evaluating performance of natural language understanding (NLU) models across a diverse set of tasks

Each dataset uses different metric(s), hence, scores are averaged to a final score

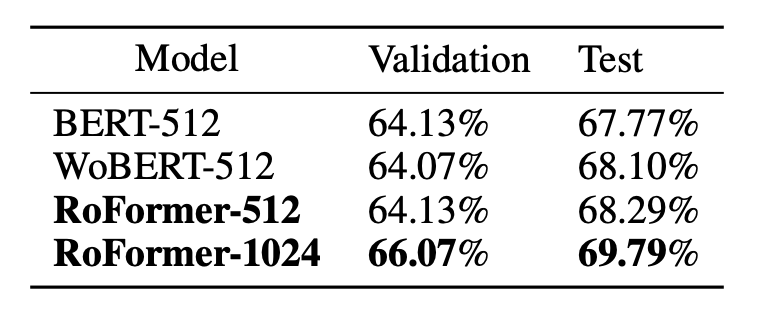
5. Handling long texts on Chinese Datasets

• Performance improves as sequence length increases

🟡 Limitations of RoPE

• Unclear why RoPE converges faster than other strategies
• Superior performance on long texts cannot be explained convincingly
  • Attributed to long-term decay, but other strategies have this property as well

RoPE Scaling

• RoPE has seen widespread adoption in modern architectures like LLaMA and Gemma
• One exciting reason is RoPE Scaling
• Main Idea: Modify the base value (10,000 by default) to allow model to handle longer sequences
• Base value is scaled using rope_factor
  • rope_factor = 2 doubles context length
  • Finding rope factor depends on task, architecture and requires experimentation
• Idea discussed better in Xiaoran Liu, et al., Scaling Laws of RoPE-based Extrapolation
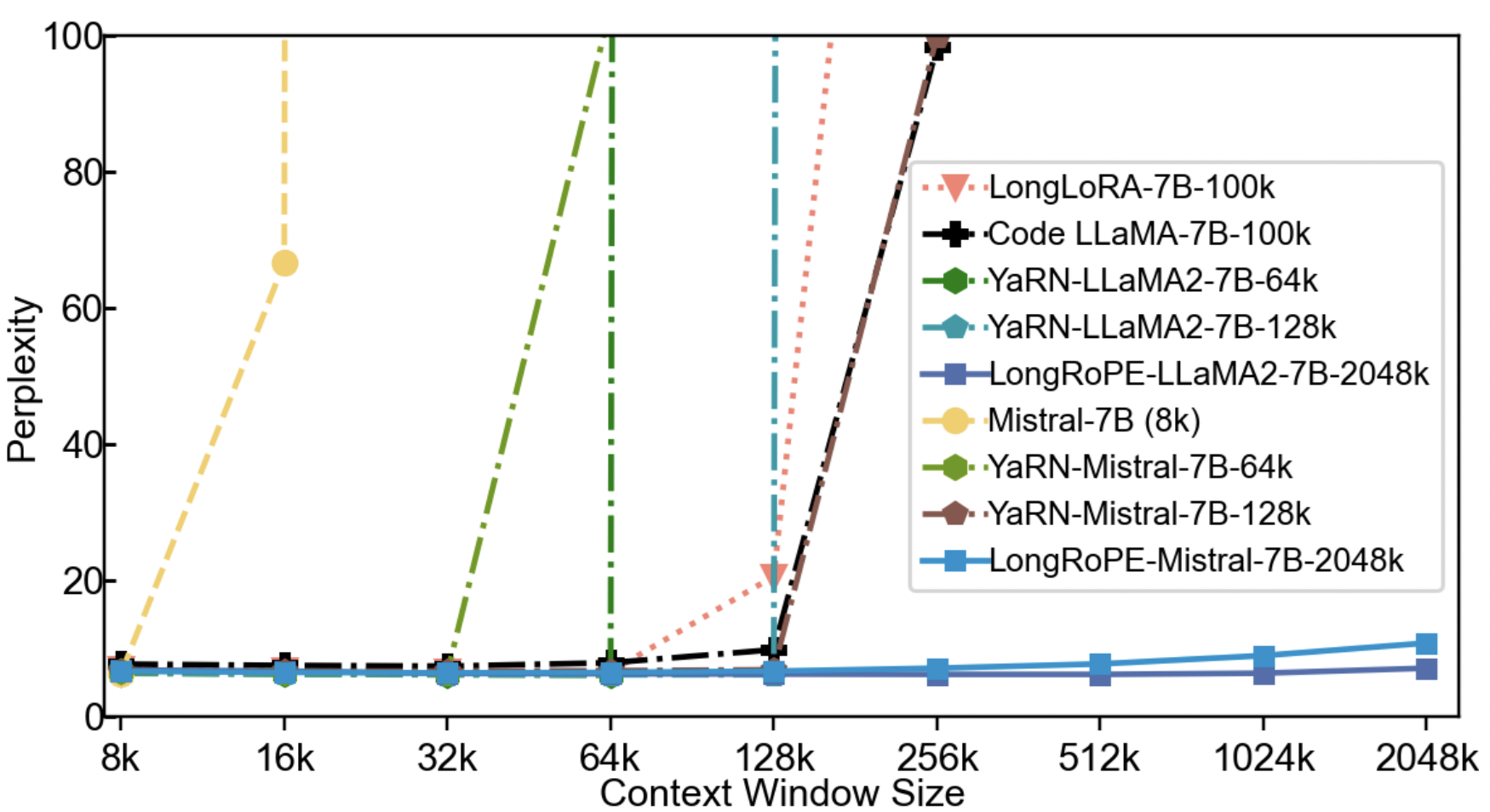
• Just by scaling base value, RoPE can be used for longer sequences, but performance degrades
  • (e.g.) Going from 4k to 32k without finetuning has been done
• Finetuning post scaling helps tackle this issue
• Another idea is to progressively scale and finetune to drastically improve context length
• ✨✨Scaling from 8k to 2048k with finetuning has been achieved

Source: Yiran Ding, et al., LongRoPE: Extending LLM Context Window Beyond 2 Million Tokens

📋 References

1. Jianlin Su, et al., RoFormer: Enhanced Transformer with Rotary Position Embedding
2. Umar Jamil, Attention is all you need (Transformer)
3. Amirhossein Kazemnejad, Transformer Architecture: The Positional Encoding
4. Efficient NLP, Rotary Positional Embeddings: Combining Absolute and Relative
5. Xiaoran Liu, et al., Scaling Laws of RoPE-based Extrapolation
6. Yiran Ding, et al., LongRoPE: Extending LLM Context Window Beyond 2 Million Tokens